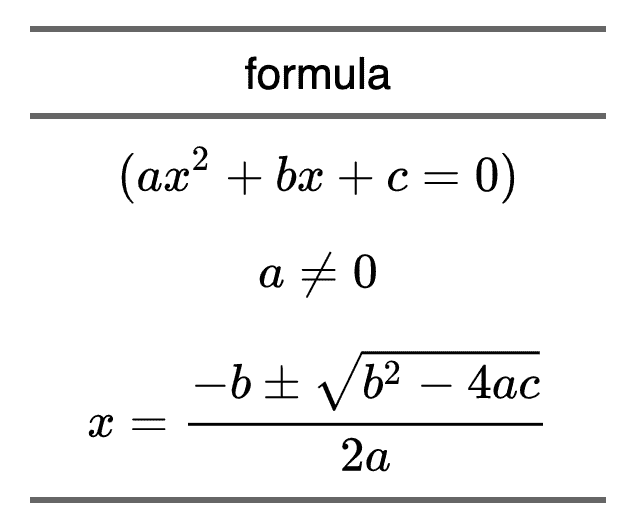Insert equations

Packages utilisés

We use the ‘equatiomatic’ package which will allow us to get the equation of the model in ‘latex’ format.

library(flextable)
library(equatiomatic)

Le flextable

We will generate a flextable from a linear model using the function as_flextable().

mod <- lm(mpg ~ cyl + disp, mtcars)
ft <- as_flextable(mod)
ft

	Estimate	Standard Error	t value	Pr(>\|t\|)
(Intercept)	34.661	2.547	13.609	0.0000	***
cyl	-1.587	0.712	-2.230	0.0337	*
disp	-0.021	0.010	-2.007	0.0542	.
Signif. codes: 0 <= '*' < 0.001 < '' < 0.01 < '*' < 0.05

Residual standard error: 3.055 on 29 degrees of freedom
Multiple R-squared: 0.7596, Adjusted R-squared: 0.743
F-statistic: 45.81 on 29 and 2 DF, p-value: 0.0000

Ajouter l’équation dans le tableau

The function equatiomatic::extract_eq() will be used to get the equation in latex format:

eq <- extract_eq(mod)
print(eq)
## $$
## \operatorname{mpg} = \alpha + \beta_{1}(\operatorname{cyl}) + \beta_{2}(\operatorname{disp}) + \epsilon
## $$

It remains finally to add it in the table with the function flextable::compose(). You have to indicate that you want to treat the value as a ‘latex’ equation by using the function as_equation().

ft <- add_header_lines(ft, "", top = TRUE)

ft <- compose(
  x = ft, j = 1, i = 1, part = "header",
  value = as_paragraph(
    as_equation(eq, 
    width = 2, height = .5)
  )
)

ft <- align(ft, i = 1, part = "header", align = "center")
ft

$\operatorname{mpg} = \alpha + \beta_{1}(\operatorname{cyl}) + \beta_{2}(\operatorname{disp}) + \epsilon$
(Intercept)	34.661	2.547	13.609	0.0000	***
cyl	-1.587	0.712	-2.230	0.0337	*
disp	-0.021	0.010	-2.007	0.0542	.
Signif. codes: 0 <= '*' < 0.001 < '' < 0.01 < '*' < 0.05

Residual standard error: 3.055 on 29 degrees of freedom
Multiple R-squared: 0.7596, Adjusted R-squared: 0.743
F-statistic: 45.81 on 29 and 2 DF, p-value: 0.0000

Another example

eqs <- c(
  "(ax^2 + bx + c = 0)",
  "a \\ne 0",
  "x = {-b \\pm \\sqrt{b^2-4ac} \\over 2a}")
df <- data.frame(formula = eqs)
df
##                                   formula
## 1                     (ax^2 + bx + c = 0)
## 2                                a \\ne 0
## 3 x = {-b \\pm \\sqrt{b^2-4ac} \\over 2a}


ft <- flextable(df)
ft <- compose(
  x = ft, j = "formula",
  value = as_paragraph(as_equation(formula, width = 2, height = .5)))
ft <- align(ft, align = "center", part = "all")
ft <- width(ft, width = 2)
ft

formula
$(ax^2 + bx + c = 0)$
$a \ne 0$
$x = {-b \pm \sqrt{b^2-4ac} \over 2a}$